Եգիպտական բուրգեր
Բուրգերի համալիրը՝ Հին Եգիպտոսի հուշարձանների համալիր, որը գտնվում է Գիզա սարահարթում,Կահիրե քաղաքի մոտակայքում։ Բուրգերից ամենամեծը՝ Քեոփսի բուրգը ունի 5 հազար տարվա պատմություն, Քյոփս փարավոնի դամբարանն է, ունի 147 մետր բարձրություն և յուրաքանչյուր կոզքի բարձրությունը 233 մետր է: Ըստ ուսումնասիրությունների բուրգի կառուցման համար օգտագործվել է երկու միլիոն երեք հարյուր հազար կրաքարային խոշոր զանգված: Դրանցից յուրաքանչյուրն էլ կշռել է երկու տոննայից ավել: Բուրգի ամենամեծ առանձնահատկությունը ուռուցիկ պատերն են: Ժայռաբեկորները այնքան ամուր և վարպետորեն են տեղադրված որ նւյնիսկ դանակի շեղբ չի անցնի: Հաշվի առնելով որ բուրգերը կառուցվել են քարե գործիքներով ապա զարմանալի է վարպետների աշխատանքի ճշտությունը:Եթե մարդիկ ցանկանում էին տեսնել մահացած փարավոնինկարող էին այցելել հոգեհանգստի տաճար՝ ընդունարան, որը կառուցված էր գրանիտե ուղղանկյուն սյուներով և հայելու նման փայլփլուն պատերով և հատակով:
Փարավոնի մարմինը պահպանելու համար զմրսում էին: Հետո փարավոնի զմռսված մարմինը զուգում-զարդարում էին, զգեստավորում շքեղ բանվածքներով, դնում կեղծամ, ոսկեզօծում եղունգները, ակնակապիճներում զետեղում փղոսկրյա կամ բյուրեղապակյա աչքեր։ Այս կերպ էր պատրաստվում մումիան։ Վերջում հոգ էին տանում, որ հանգուցյալը հանդերձյալ կյանքում ապահովված լինի արդուզարդով, անոթներով, ըմպանակներով, կառքով։
Մինչև այժմ էլ գիտնականները չեն կարողացել բացահայտել բուրգերի գաղտնիքը: Այն մինչև հիմա էլ գիտնականների սւշադրության կենտրոնում է: Գիտնականներին էլ շատ է հետաքրքրում թե առանց տեխնիկայի եգիպտացիներն ինխպես են կարողացել ճշգրիտ կառուցել այդ հսկա բուրգերը:
Նորվեգական ինստիտուտի ճարտարապետ Օլե Բրինը բուրգերի գաղտնիքների բացահայտման նոր ուղիներ է առաջարկել:
Ըստ նորվեգացի գիտնականի կառույցի շինարարական գաղտնիքն ավելի պարզ է քան տվում է: Եգիպտացիները օգտագործել են «կոտրող ցանց», որն օգտագործվում է նաև ժամանակակից շինարարության մեջ: Այդ ցանցի էությունը հետևյալն է, ընտրվում է որոշակի կենտրոն, դրանից դուրս են գալիս որոշակի առանցքներ ու բարդ, բայց համաչափ կառույցի շինարարության համար պահանջվում է պարզապես ճշգրտորեն պահպանել ու հետևել աղյուսների միջև ընկած հեռավորությանը: Բրինի կարծիքով եգիպտացիներն իրենց բոլոր հաշվարկների համար ընտրել էին 7 թիվը: Այս տվից օգտվելը բավականին հեշտ է:
Գիտնականները համոզված են որ եգիպտացիներըկազմում էին գծագրեր որոնցով էլ ճշգրիտ կառույցներ էին կառուցում:
Քեոփսի բուրգը մարդկության համար մնում է ամենաառեխծվածային գաղտնիքներից մեկը:
Եգիպտական բուրգերի
գաղտնիքները
Գիտնականները գիտեն բոլոր միջոցները, որոնք օգտագործել են հին եգիպտացիները, որպեսզի մի քանի տոննա կշռող քարերը երկրի հարավում գտնվող Ասուանից տեղափոխեն ներկայիս Կահիրեի մոտ գտնվող Գիզայի բուրգերը կառուցելու համար: Ռիա նովոստիի հաղորդմամբ, արաբական Աշ Շարկ ալ Աուսաթ թերթին եգիպտացի հնագետ և Եգիպտոսի հնությունների գծով նախկին նախարար Զահի Հավասն ասել է, որ ժամանակակից գիտության համար որևէ գաղտնիք այդ պրոցեսում չկա:
Նախօրեին բրիտանական Daily Mail-ը հոդված էր հրապարակել, որում նշվում էր, որ հնագետների խումբը հնագույն պապիրուսի օգնությամբ բացահայտել էր բուրգերի շինարարության գաղտնիքը: Փաստաթղթում մանրամասն ներկայացված է մեթոդը, որը եգիպտացիներն օգտագործել են ավելի քան 4600 տարի առաջ ծանր գրանիտե բլոկները ավելի քան 800 կիլոմետր տեղափոխելու համար: Պապիրուսում մասնավորապես պատմվում է, որ տեղափոխման համար օգտագործվել են հատուկ շինարարական ջրանցքներ:
«Տեղափոխումն իրականացվել է Ասուանի մոտ գտնվող քարի մշակման վայրի հատուկ նավահանգստից՝ փայտե նավակներով, որոնք շարժվել են Նեղոսով, հետո շինարարական ջրանցքներով հասել են մինչև բուրգերի մոտ գտնվող նավահանգիստ»,- ասել է Զահի Հավասը:
Գիզայի բուրգերի հնագիտական համալիրը գտնվում է Նեղոսի ափին՝ Կահիրեի մոտ: Համալիրն ավելի քան 4,5 հազար տարեկան է և բաղկացած է երեք խոշոր բուրգերից՝ Քեոփսի, Քեֆրենի և Միքերինի:
Գլանի և կոնի
մասին
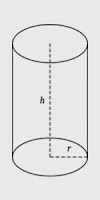
Գլան
V = Sհ*H = πR2H
Sկ = 2πRH
Sլր = Sկ + 2Sհ = 2πRH + 2πR2 =>
Sլր = 2πR(H + R)
V = Sհ*H = πR2H
Sկ = 2πRH
Sլր = Sկ + 2Sհ = 2πRH + 2πR2 =>
Sլր = 2πR(H + R)
Կոն
V = 1/3 Sh*H = 1/3 πR2H
Sկ = πRl
Sլր = Sկ + Sհ = πRl + πR2 =>
Sլր = πR(l + R)










Комментариев нет:
Отправить комментарий